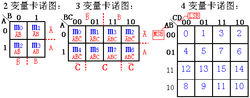
卡诺图(Karnaugh map)是逻辑函数的一种图形表示,由莫里斯·卡诺(Maurice Karnaugh)发明。一个逻辑函数的卡诺图就是把该函数最小项表达式中的各最小项相应地填入一个方格图内,方格图称为卡诺图。卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最小项,两个相邻最小项可以合并为一个与项并消去一个变量。
发展历史
组合电路逻辑关系的图形表示法可以追溯到英国逻辑学家约翰·维恩(John Venn)1881年发明的在集合论中处理集合间逻辑关系的文氏图(Venn diagram),赫尔姆·哈斯(Helmut Hasse)有效地利用Vogt在1895年用过的哈斯图(Hasse diagram)来表示序理论中的有限偏序集,爱德华·维奇(Edward W. Veitch)在1952年将维恩图中的圆形改画成矩形而发明了维奇图(Veitch diagram)。但这些图都不如美国贝尔实验室的电信工程师莫里斯·卡诺(Maurice Karnaugh)在1953年根据维奇图改进的卡诺图(Karnaugh map)或K图(K-map)在数字逻辑、故障诊断等许多领域中应用广泛。
化简法
由于卡诺图两个相邻最小项中,只有一个变量取值不同,而其余的取值都相同。所以,合并相邻最小项,利用公式A+A=1,AB+AB=A,可以消去一个或多个变量,从而使逻辑函数得到简化。
(1)卡诺图中最小项合并的规律合并相邻最小项,可消去变量。合并两个最小项,可消去一个变量;合并四个最小项,可消去两个变量;合并八个最小项,可消去三个变量;合并2N个最小项,可消去N个变量。
(2)利用卡诺图化简逻辑函数 A.基本步骤: ① 画出逻辑函数的卡诺图; ② 合并相邻最小项(圈组); ③ 从圈组写出最简与或表达式。关键是能否正确圈组 。 B.正确圈组的原则 ① 必须按2、4、8、2N的规律来圈取值为1的相邻最小项; ② 每个取值为1的相邻最小项至少必须圈一次,但可以圈多次; ③ 圈的个数要最少(与项就少),并要尽可能大(消去的变量就越多)。 C.从圈组写最简与或表达式的方法: ① 将每个圈用一个与项表示圈内各最小项中互补的因子消去,相同的因子保留,相同取值为1用原变量,相同取值为0用反变量; ② 将各与项相或,便得到最简与或表达式。圈组技巧(防止多圈组的方法): ① 先圈孤立的1; ② 再圈只有一种圈法的1; ③ 最后圈大圈; ④检查:每个圈中至少有一个1未被其它圈圈过。
变量
表示各最小项的2^n(n-变量数)个小格,排列呈矩形。
小格按“循环码” 排列,保证最小项间“几何相邻”与“逻辑相邻性”的统一。(几何相邻有“内相邻” “外相邻”和“中心对称”)
化简函数
1.几个定义
蕴涵项:在函数的“与-或”表达式中,每个“与”项被称为该函数的蕴涵项(Implicant)。
显然,在函数卡诺图中,任何一个1方格所对应的最小项或者卡诺圈中的2m个1方格所对应的“与”项都是函数的蕴涵项。
质蕴涵项:若函数的一个蕴涵项不是该函数中其他蕴涵项的子集,则此蕴涵项称为质蕴涵项(Prime Implicant),简称为质项。
显然,在函数卡诺图中,按照最小项合并规律,如果某个卡诺圈不可能被其他更大的卡诺圈包含,那么,该卡诺圈所对应的“与”项为质蕴涵项。
必要质蕴涵项:若函数的一个质蕴涵项包含有不被函数的其他任何质蕴涵项所包含的最小项,则此质蕴涵项被称为必要质蕴涵项(Essential Prime Implicant),简称为必要质项。
在函数卡诺图中,若某个卡诺圈包含了不可能被任何其他卡诺圈包含的1方格,那么,该卡诺圈所对应的“与”项为必要质蕴涵项。
2.求函数最简“与-或”表达式
(1)一般步骤: 第一步:作出函数的卡诺图。
第二步:在卡诺图上圈出函数的全部质蕴涵项。按照卡诺图上最小项的合并规律,对函数F卡诺图中的1方格画卡诺圈。为了圈出全部质蕴涵项,画卡诺圈时在满足合并规律的前题下应尽可能大,若卡诺圈不可能被更大的卡诺圈包围,则对应的“与”项为质蕴涵项。
第三步:从全部质蕴涵项中找出所有必要质蕴涵项。在卡诺图上只被一个卡诺圈包围的最小项被称为必要最小项,包含必要最小项的质蕴涵项即必要质蕴涵项。为了保证所得结果无一遗漏地复盖函数的所有最小项,函数表达式中必须包含所有必要质蕴涵项。
第四步:求出函数的最简质蕴涵项集。若函数的所有必要质蕴涵项尚不能复盖卡诺图上的所有1方格,则从剩余质蕴涵项中找出最简的所需质蕴涵项,使它和必要质蕴涵项一起构成函数的最小复盖。
归纳起来,卡诺图化简的原则是:
☆ 在复盖函数中的所有最小项的前提下,卡诺圈的个数达到最少。
☆ 在满足合并规律的前提下卡诺圈应尽可能大。
☆ 根据合并的需要,每个最小项可以被多个卡诺圈包围。
3.求函数的最简“或-与”表达式
当需要求一个函数的最简“或-与”表达式时,可采用“两次取反法”。
具体如下:
☆ 先求出函数F的反函数F的最简“与-或”表达(合并卡诺图上的0方格);
☆ 然后对F的最简“与-或”表达式取反,从而得到函数F的最简“或-与”表达式。
卡诺图化简逻辑函数具有方便、直观、容易掌握等优点。但依然带有试凑性。尤其当变量个数大于6时,画图以及对图形的识别都变得相当复杂。
原创文章,作者:来自网友投稿,如若转载,请注明出处:https://www.ladyww.cn/article/20221212120793.html