余弦定理,欧氏平面几何学基本定理。余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广,勾股定理是余弦定理的特例。余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求三角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
发展简史
16世纪三角函数表的制作首推奥地利数学家雷蒂库斯(G.J.Rhetucus,1514~1574)。他1536年毕业于滕贝格(Witten bery)大学,留校讲授算术和几何。1539年赴波兰跟随著名天文学家哥白尼学习天文学,1542年受聘为莱比锡大学数学教授.雷蒂库斯首次编制出全部6种三角函数的数表,包括第一张详尽的正切表和第一张印刷的正割表。
17世纪初对数发明后大大简化了三角函数的计算,制作三角函数表已不再是很难的事,人们的注意力转向了三角学的理论研究。不过三角函数表的应用却一直占据重要地位,在科学研究与生产生活中发挥着不可替代的作用。三角公式是三角形的边与角、边与边或角与角之间的关系式。三角函数的定义已体现了一定的关系,一些简单的关系式在古希腊人以及后来的阿拉伯人中已有研究。
文艺复兴后期,法国数学家韦达(F.Vieta)成为三角公式的集大成者.他的《应用于三角形的数学定律》(1579)是较早系统论述平面和球面三角学的专著之一。其中第一部分列出6种三角函数表,有些以分和度为间隔。给出精确到5位和10位小数的三角函数值,还附有与三角值有关的乘法表、商表等。第二部分给出造表的方法,解释了三角形中诸三角线量值关系的运算公式.除汇总前人的成果外,还补充了自己发现的新公式,如正切定律、和差化积公式等等。他将这些公式列在一个总表中,使得任意给出某些已知量后,可以从表中得出未知量的值。该书以直角三角形为基础。对斜三角形,韦达仿效古人的方法化为直角三角形来解决,对球面直角三角形,给出计算的完整公式及其记忆法则,如余弦定理,1591年韦达又得到多倍角关系式,1593年又用三角方法推导出余弦定理。
1722年英国数学家棣莫弗(A.De Meiver)得到以他的名字命名的三角学定理,并证明了是正有理数时公式成立;1748年欧拉(L.Euler)证明了是任意实数时公式也成立,他还给出另一个著名公式,对三角学的发展起到了重要的推动作用。
近代三角学是从欧拉的《无穷分析引论》开始的。他定义了单位圆,并以函数线与半径的比值定义三角函数,他还创用小写拉丁字母表示三角形三条边,大写拉丁字母表示三角形三个角,从而简化了三角公式。使三角学从研究三角形解法进一步转化为研究三角函数及其应用,成为一个比较完整的数学分支学科。而由于上述诸人及19世纪许多数学家的努力,形成了现代的三角函数符号和三角学的完整的理论。
定理定义
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
验证推导
证法一
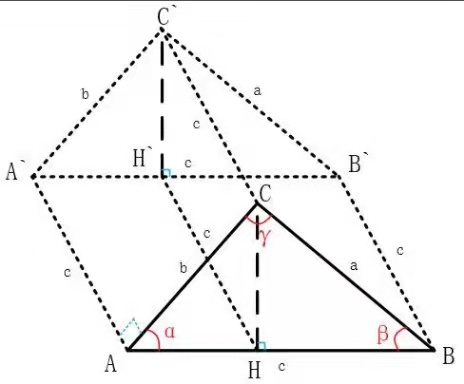
如图所示,,在上做高
将边写:
将等式同乘以得到:
如图所示:以边为边长,以垂直于面作向里的正方形辅助线,然后作平行于`边的`等,则,上述公式相当于辅助正方形的面积等于长方形和在正方形`中的投影面积(分别为与)之和。
对另外两边分别作高,运用同样的方法可以得到:
将两式相加:
证法二
在中,,
在中,
正弦定理证法
在中,
(降幂公式)
(和差化积)
(降幂公式)
(以及诱导公式)
(和差化积)(由此证明余弦定理角元形式)
设的外接圆半径为
∴
∴(正弦定理)
∴
平面向量证法
(粗体字符表示向量)
又 (诱导公式)
此即
即
同理可证其他,而下面的 就是将移到左边表示一下。
定理推广
求边
余弦定理公式可变换为以下形式:
因此,如果知道了三角形的两边及其夹角,可由余弦定理得出已知角的对边。
求角
因为余弦函数在[0,π]上的单调性,可以得到:
求面积
由面积公式
知如果已知三角形的三条边,可以由余弦定理求出一个内角,从而得到三角形的面积。
定理意义
余弦定理是解三角形中的一个重要定理,可应用于以下三种需求:
当已知三角形的两边及其夹角,可由余弦定理得出已知角的对边。
当已知三角形的三边,可以由余弦定理得到三角形的三个内角。
当已知三角形的三边,可以由余弦定理得到三角形的面积。
原创文章,作者:来自网友投稿,如若转载,请注明出处:https://www.ladyww.cn/article/20230426148604.html